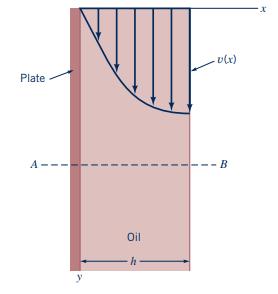
A layer of oil flows down a vertical plate as shown in Fig P4 63 with a velocity of ( mathbf V left(V 0 h 2 ight) left(2 h x x 2 ight) hat mathbf j ) where (V 0 ) and (h ) are constants (a) Show that the fluid sticks to the plate and that the shear stress at the edge of the layer ((x h) ) is zero (...

The Answer is in the image, click to view ...

A layer of oil flows down a vertical plate as shown in Fig. P4.63 with a velocity

Question:

A layer of oil flows down a vertical plate as shown in Fig. P4.63 with a velocity of $\mathbf{V}=\left(V_{0} / h^{2}\right)\left(2 h x-x^{2}\right) \hat{\mathbf{j}}$ where $V_{0}$ and $h$ are constants.

(a) Show that the fluid sticks to the plate and that the shear stress at the edge of the layer $(x=h)$ is zero.

(b) Determine the flowrate across surface $A B$. Assume the width of the plate is $b$. The velocity profile for laminar flow in a pipe has a similar shape.

Figure P4.63