Stokes's first problem involves the instantaneous acceleration at time (t=0) of a flat plate to a constant

Question:

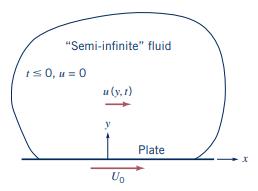
"Stokes's first problem" involves the instantaneous acceleration at time \(t=0\) of a flat plate to a constant velocity \(U_{0}\) while in contact with a "semi-infinite," static fluid as shown in Fig. P6.70. For a constant fluid density and viscosity, the simplified NavierStokes equation is

\[ \frac{\partial u}{\partial t}=u \frac{\partial^{2} u}{\partial y^{2}} \]

where \(u\) is the fluid velocity in the \(x\) or velocity \(U_{0}\) direction and \(y\) is a coordinate normal to the plate. Find the appropriate boundary conditions and initial conditions for this problem and then solve the differential equation to determine the velocity distribution \(u / U_{0}=f(y, t)\). Assume that \(f\) is a function of a single variable \(\eta\) where \(\eta=y / 2 \sqrt{u t}\).

Figure P6.70