The pressure rise, \(\Delta p\), across a centrifugal pump of a given shape can be expressed as

\[ \Delta p=f(D, \omega, ho, Q) \]

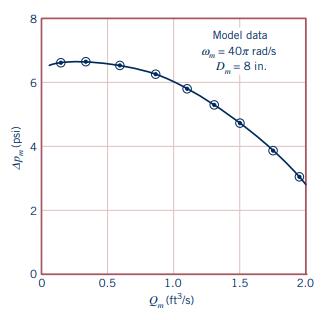
where \(D\) is the impeller diameter, \(\omega\) the angular velocity of the impeller, \(ho\) the fluid density, and \(Q\) the volume rate of flow through the pump. A model pump having a diameter of 8 in. is tested in the laboratory using water. When operated at an angular velocity of \(40 \pi \mathrm{rad} / \mathrm{s}\) the model pressure rise as a function of \(Q\) is shown in Fig. P8.72. Use this curve to predict the pressure rise across a geometrically similar pump (prototype) for a prototype flowrate of \(6 \mathrm{ft}^{3} / \mathrm{s}\). The prototype has a diameter of \(12 \mathrm{in}\). and operates at an angular velocity of \(60 \pi \mathrm{rad} / \mathrm{s}\). The prototype fluid is also water.

Figure P7.72

Transcribed Image Text:

00 8 6 Model data =40x rad/s D= 8 in. 4 (sd) "dy 2 0.5 1.0 1.5 2.0 Q (ft/s)