Question: The modified equations of certain finite difference schemes are given below. In each case, determine the order of approximation, and find whether the dominant error

The modified equations of certain finite difference schemes are given below. In each case, determine the order of approximation, and find whether the dominant error is due to numerical dissipation or numerical dispersion: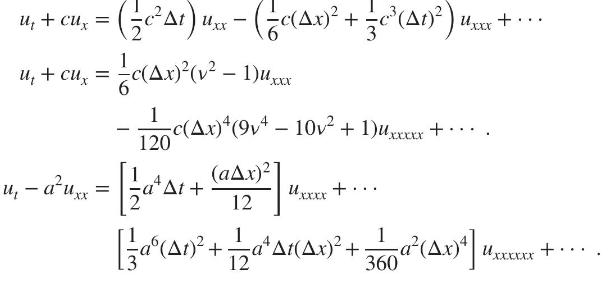 u + cu = (c At) uxx - (c (Ax) + =

u + cu = (c At) uxx - (c (Ax) + = c (At)) us u + cu = c (Ax) (v = 1) ux 1 - Uxxx + - 120 (Ax) + (9v+ - 10v + 1)Uxxxx + (aAx)2 M ... - u = auxx = [ a + = [a At + 12 [a (At) + 1 12 1 360 * At(Ax) + 3a (Ax)*] +.... u

Step by Step Solution

★★★★★

3.38 Rating (167 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Engineering Mechanics Dynamics Questions!

can someone solve this Modern workstations typically have memory systems that incorporate two or three levels of caching. Explain why they are designed like this. [4 marks] In order to investigate...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

This question comes from a Partial Differential Equation Class. The textbook we use is "Introduction to Partial Differential Equations A Computational Approach," 29 edition by Aslak Tveito and Ragnar...

function LAB04ex1 %NOTE: you CAN run this type of function m file as a script because it requires no inputs. Click the Green arrow above the "Run" tab t0 = 0; tf = 40; %initial and final time y0 =...

Python and most Python libraries are free to download or use, though many users use Python through a paid service. Paid services help IT organizations manage the risks associated with the use of...

MATLAB sessions: Laboratory 4 MAT 275 Laboratory 4 MATLAB solvers for First-Order IVP In this laboratory session we will learn how to 1. Use MATLAB solvers for solving scalar IVP 2. Use MATLAB...

Math 104A Homework #3 Instructor: Lihui Chai General Instructions: Please write your homework papers neatly. You need to turn in both full printouts of your codes and the appropriate runs you made....

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

PowerPoint Assignment for BUS 401: Principles of Finance You have been asked by a manager in your organization to put together a training program explaining Net Present Value (NPV) and Future Value...

Based on their compositions and structures and on conjugate acid-base relationships, select the stronger base in each of the following pairs: (a) BrO- or ClO-, (b) BrO- or BrO2-, (c) HPO42- or H2PO4-.

For each of the following ions, indicate the total number of protons and electrons in the ion. For the positive ions in the list, predict the formula of the simplest compound formed between each...

What is the current yield on a 6 % bond with a current market price of $ 9 0 7 ? 5 . 2 7 % 5 . 0 2 % 6 . 6 2 % 6 . 0 2 % 7 . 5 7 %

You have strayed from your party in trackless timber. You have no special signalling equipment. The best way to contact your friends is to: a. Call "help" loudly but in a low register. b. Yell or...

The cart impacts the safety barrier with speed v 0 = 3.25 m/s and is brought to a stop by the nest of nonlinear springs which provide a deceleration a = k 1 x k 2 x 3 , where x is the amount of...

The graph shows the rectilinear acceleration of a particle as a function of time over a 12-second interval. If the particle is at rest at the position s 0 = 0 at time t = 0, determine the velocity of...

Use the following to answer questions 1-4 Determine whether the firm reports each of the following items as part of cash, cash equivalents, or neither in the balance sheet Item Cash, Cash equivalent,...

ABC Co is considering using a lockbox system. The use of the system will reduce collection time by 2.5 days. The company receives on an average 760 cheques everyday with average value of each cheque...

XYZ Corporation is a multinational company operating in various sectors, including manufacturing, technology, and services. With a diverse range of operations, the company has a complex financial...