Consider a one dimensional harmonic oscillator of Hamiltonian where x and p are Lagrange conjugate variables. 1.We
Question:
Consider a one dimensional harmonic oscillator of Hamiltonian
where x and p are Lagrange conjugate variables.
1.We set x = X/ √mω and p = P √mω.
Write the expression of the Hamiltonian in terms of X and P, and calculate the Poisson bracket {X, P}.
2.We introduce the functions a and a∗, the complex conjugate of
a, defined by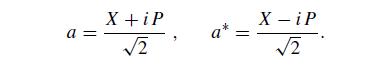
Write the Hamiltonian in terms of
a, a∗ and ω.
3.Calculate the Poisson bracket {a, a∗}.
4.Write the time evolution equation of a and give its general solution.
Write the energy E of the oscillator in terms of the parameters of this solution and of ω.
5.We assume the energy of the oscillator is zero for t ≤ 0, E(t ≤ 0) = 0.
Between t = 0 and t = T one applies to the oscillator a force which derives from the potential energy Hpot = b √2X sin (Ωt) (Hpot = 0 if t ≤ 0 or t > T ) where b is a parameter. Calculate the energy E of the oscillator for t > T .
6.Discuss the variation of E′ as a function of the exciting frequency Ω.
Step by Step Answer:






