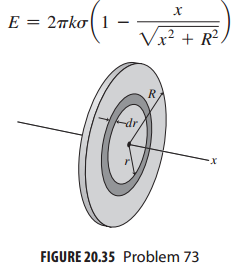
Figure 20.35 shows a thin, uniformly charged disk of radius R. Imagine the disk divided into rings of varying radii r, as suggested in the figure.  
(a) Show that the area of such a ring is very nearly 2πr dr.
(b) If the disk carries surface charge density σ, use the result of part (a) to write an expression for the charge dq on an infinitesimal ring.
(c) Use the result of (b) along with the result of Example 20.6 to write the infinitesimal electric field dE of this ring at a point on the disk axis, taken to be the positive x-axis.
(d) Integrate over all such rings to show that the net electric field on the axis has magnitude