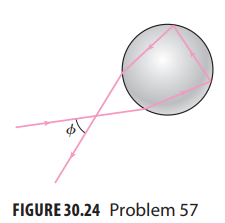
Figure 30.24 shows the approximate path of a light ray that undergoes internal reflection twice in a spherical water drop. Repeat Problems 55 and 56 for this case to find the angle at which the secondary rainbow occurs.

?

Data From Problem 55 & 56?

55. Figure 30.23 shows light passing through a spherical raindrop, undergoing two refractions and total internal reflection, resulting in an angle f between the incident and outgoing rays. Show that f = 4 sin^-1 (sin ?/n) - 2?, where ? is the incidence angle.

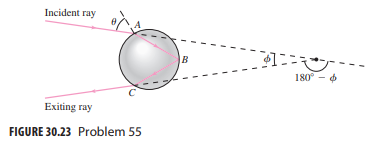
56. (a) Differentiate the result of Problem 55 to show that the maximum value of ? occurs when the incidence angle ? is given by cos²? = 1/3 (n² ? 1). (b) Use this result and that of Problem 55 to find the maximum ? in a raindrop with n = 1.333. This is the angle at which the rainbow appears, as shown in the Application on pages 573?574.

Transcribed Image Text:

FIGURE 30.24 Problem 57