The derivation of Equation (6.1) relies on the method of canceling units in brackets [. . .]
Question:
The derivation of Equation (6.1) relies on the method of canceling units in brackets [. . .] as in the following steps. Replace each of the steps in words with its dimensionally correct mathematical equivalent, and so derive the Otto Cycle Power Output Equation.
Step 1: How much air is drawn into the cylinder? The actual volume of air drawn into the cylinder is D as the piston cycles from top dead center to the bottom dead center. The mass of air drawn into the cylinder is thus . . .?
Step 2: How much fuel? Use (F/A)Mass ratio.
Step 3: How much thermal energy is released by this amount of fuel for just one power stroke?
Needs the HV of the fuel
Step 4: Of this heat, only a portion is converted into mechanical work. The mechanical work is related to the thermal input by ZOtto.
Step 5: How many power strokes are there? As we have seen, there is just one per every two engine revolutions, and N is the number of revolutions/minute. Multiply the mechanical work by number of power strokes/s.
Step 6: Hence, the rate of working is ηOtto × [ρrair × D × (A/F)Mass] × HV × N/(2 × 60) [kJ of work per power stroke] [power strokes per second] = [kJ (work)/s] = [kW].
Step 7: Finally, cast this in the suggested form:
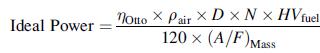
Step by Step Answer:

Exploring Engineering An Introduction to Engineering and Design
ISBN: 978-0123747235
2nd edition
Authors: Philip Kosky, George Wise, Robert Balmer, William Keat





