Starting with an equilateral triangle, a Koch snowflake pattern can be constructed using the following steps:

Step 1: Divide each line segment into three equal segments.

Step 2: Draw an equilateral triangle, pointing outward, which has the middle segment from step 1 as its base.

Step 3: Remove the line segments that were used as the base of the equilateral triangles in step 2.

These three steps are then repeated to produce the next pattern.

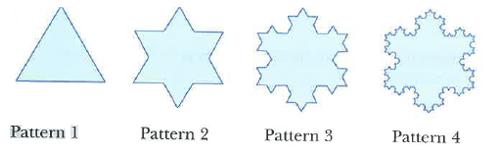
You are given that the triangle in pattern 1 has side length x units.

a. Find in terms of x, expressions for the perimeter of each of patterns 1, 2, 3 and 4 and explain why this progression for the perimeter of the snowflake diverges to infinity.

b. Show that the area of each of patterns 1, 2, 3 and 4 can be written as

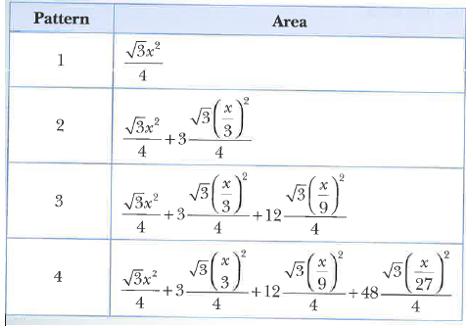
Hence show that the progression for the area of the snowflake converges to 8/5 times the area of the original triangle.

Transcribed Image Text:

Pattern 1 Pattern 2 Pattern 3 Pattern 4