1.) To appreciate the subtle issues that we may face in financial model calibration, imagine the task of calibrating a short-rate model, like Vasicek or CIR. A simple approach could be to collect a set of prices of zero-coupon bonds with a range of maturities, for which we have analytical pricing formulas, and solve the nonlinear least-squares problem (14.56). This requires finding a set of liquid zeros with comparable risk (actually, they should be risk-free).
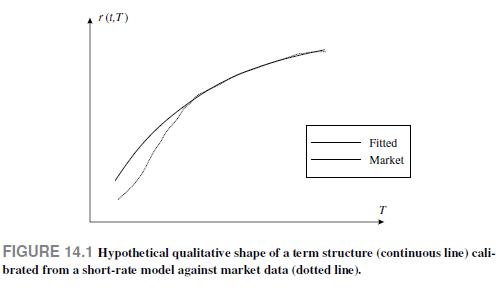
As a check, we should verify the fit between the observed term structure of interest rates, which is implicit in the bond prices, and the one generated by the model. Imagine that we obtain the term structure depicted in Fig. 14.1. As one should expect, the fit is not perfect, since we have used a single-factor model. However, we do note a pattern, as the lack of fit is not uniform across maturities. It seems that the long term rates are matched well enough, whereas the shorter term rates leave much to be desired. Is there an explanation for this pattern?
We may find an explanation in terms of bond duration. The zeros with long maturities have a large duration, and their prices are quite sensitive to changes in yield. Hence, the calibration should really match the long term rates well. On the contrary, the zeros with smaller duration are less sensitive, and a mismatch in term of underlying interest rates does not affect the quality of the calibration, which is carried out in term of prices, not rates.

Data From problem (14.56)

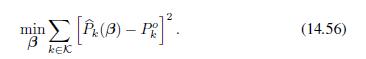
Data From Fig. 14.1

Transcribed Image Text:

mign [P.() - P] kK 2 (14.56)