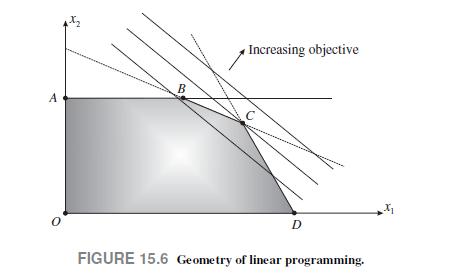
Figure 15.6 shows a possible feasible set for an LP where we maximize an objective function with respect to two decision variables, x1 and x2. A polyhedron like this may be generated by three linear inequalities and two sign restrictions on the decisions. We show the level curves of the objective, which are parallel lines in an LP problem. The optimal solution corresponds to the extreme point C.

A change in the coefficients of the objective function would imply a rotation of the level curves, so that the optimal solution would shift to B or D. Note that when the level curves are parallel to a face of the polyhedron, we have multiple optima (actually, a whole edge of them).

Data From Fig 15.6

Transcribed Image Text:

A B Increasing objective D FIGURE 15.6 Geometry of linear programming.