As at the end of Sect. 4.4, consider an arbitrage free financial market with a firm operating in two dates \(t \in\{0,1\}\). Denote by \(V_{1}\) the revenues of the firm at date \(t=1\) and suppose that the net firm profits are taxed, in the sense that at date \(t=1\) the following tax has to be payed:

\[T_{1}\left(\omega_{s}\right):=\tau\left(V_{1}\left(\omega_{s}\right)-K\right)^{+}\]

for any \(s=1, \ldots, S\), where \(\tau>0\) represents a tax rate and \(K \geq 0\) is the nominal value of the firm debt. In particular, if \(K=0\) (unleveraged firm), then the tax to be payed at \(t=1\) is simply equal to \(\tau V_{1}\left(\omega_{s}\right)\), for \(s=1, \ldots, S\). We denote by \(V_{0}^{\mathrm{un}, \text { tax }}\) the value at date \(t=0\) of an unleveraged firm subject to taxation. On the other hand, if \(K>0\) (leveraged firm), then we denote by \(V_{0}^{\mathrm{lv}, \operatorname{tax}}\) the value at \(t=0\) of a leveraged firm and by \(B_{t}\) the market value of the debt at date \(t\), for \(t \in\{0,1\}\). Assume that both the firm equity and debt are traded in the financial market. Prove that the value at date \(t=0\) of a leveraged firm subject to taxation is given by

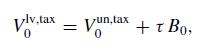
where \(V_{0}^{\mathrm{un}, \text { tax }}\) denotes the market value at \(t=0\) of an unleveraged firm subject to taxation. In particular, the value of a leveraged firm subject to taxation is increasing with respect to the market value of the debt.

Transcribed Image Text:

Vun,tax + Bo, Vlv.tax 0 0