Common wisdom suggests that increasing correlation between risk sources has an adverse effect on investors. Actually, there may be somewhat paradoxical results. Imagine an \(\mathrm{ABS}\) (or a CDO), where loss is related to default on the part of 100 debtors, and all potential losses are the same in monetary terms. The probability of default is \(2 \%\) for each debtor. Consider an equity tranche liable to pay the first \(5 \%\) of defaults. What is the probability of losing the whole value of the asset?

If default events are both equiprobable and independent, the probability distribution of the number \(X\) of defaults is a binomial random variable, with probability 0.02 and size 100 . The probability of a total loss for the equity tranche is

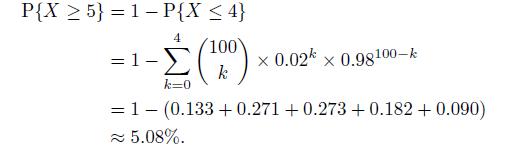
If correlation is increased to 1, i.e., in the case of perfect correlation, there are only two scenarios:

- A name defaults, hence, all of them do the same, with probability \(2 \%\), which is the probability of total loss.

- No one defaults, with probability \(98 \%\).

Therefore, we notice that increasing the correlation reduces the risk of losing the whole value of an equity tranche asset, contrary to common wisdom.

Remark. We notice that we are using the term "correlation" in a somewhat improper way, as the correlation coefficient refers to values of numerical random variables, whereas we are talking about correlation of events. The meaning can be made more precise, but we disregard these technical issues.

On the contrary, a senior tranche covering the last \(80 \%\) of defaults is fairly safe with independent defaults, as the probability of observing more than 20 defaults is negligible. However, total loss has probability \(2 \%\) in the case of perfect correlation. Hence, an increasing correlation increases risk in this case, as one would expect.

Clearly, this example is a limit case, but it shows that the effect of correlation risk may be counterintuitive.

Transcribed Image Text:

P{X5} 1- P{X 4} 1. 4 =1-(100) 0.02 x 0.98 100-k - k=0 k x = 1 (0.133 +0.271 +0.273 +0.182 + 0.090) 5.08%.