Consider a weird derivative with the payoff \(W_{T}\) depicted in Fig. 2.5, depending on the price \(S_{T}\) of a certain underlying asset at time \(t=T\). The breakpoint prices, \(K_{1}

\[K_{2}=\frac{K_{1}+K_{3}}{2}\]

The payoff is piecewise linear, and the slopes on the range with strictly positive payoff are +1 and 1 . This payoff corresponds to a common trading strategy, called butterfly spread. When \(K_{2}\) is close to the current price \(S_{0}\) of the underlying asset, the strategy is essentially a bet on low volatility, i.e., we make a profit if the asset price does not move away from \(S_{0}\). Now imagine that, at time \(t=0\), three call options on the same asset are available, with strike prices \(K_{1}, K_{2}\), and \(K_{3}\), respectively. These three options mature at time \(t=T\), and let \(C_{i}(0), i=123\) denote their prices.

It is easy to see that the butterfly spread may be synthesized by taking a long position in one option with strike \(K_{1}\), a long position in one option with strike \(K_{3}\), and a short position in two options with strike \(K_{2}\). To see this, observe that the value of the portfolio of call options matches the butterfly spread for any price \(S_{T}\). This is summarized in Table 2.3. When \(S_{T})\), the first option has a positive payoff (we say that it is in-the-money), and the total payoff is \(S_{T} \quad K_{1}\). The other cases are treated similarly, as shown in Table 2.3. Summing the payoffs of the three options in each possible case yields the payoff of Fig. 2.5.

Therefore, we have a portfolio and an asset with the same value in each possible state in the future. Then, by the law of one price, the initial value of the asset must be the initial value of the portfolio,

\[C_{1}(0) \quad 2 C_{2}(0)+C_{3}(0)\]

no more, no less. Otherwise, the law of one price would be violated and we could make an immediate profit by shorting the more expensive portfolio and buying the cheaper one, knowing that we will always break even at maturity. In this case, we would essentially buy a portfolio with a negative initial value, which means that we earn a profit by buying it, but with zero value (no commitment at all) for the future.

Data From Figure 2.5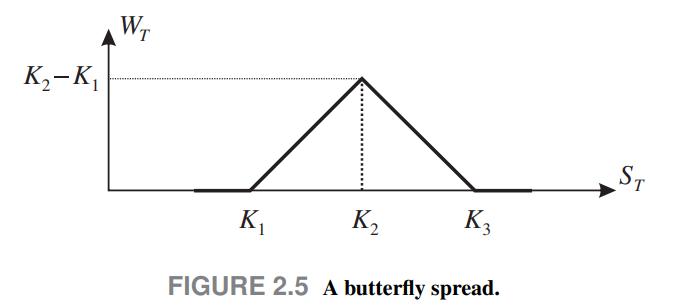

Data From Table 2.3

Transcribed Image Text:

K-K WT ST K K K3 FIGURE 2.5 A butterfly spread.