Consider the De Long et al. [549] model introduced in Sect. 9.3 and extended as in De Long et al. [549, Section III.B] to the case where the risky asset yields at each date \(t \in \mathbb{N}\) a dividend \(d_{t}\) equal to

\[d_{t}=r_{f}+\tilde{\varepsilon}_{t}, \quad \text { for all } t \in \mathbb{N}\]

where \(\left(\tilde{\varepsilon}_{t}\right)_{t \in \mathbb{N}}\) is a sequence of i.i.d. normal random variables with zero mean and constant variance \(\sigma_{\varepsilon}^{2}\), independent of the noise traders' misperceptions \(\left(\varrho_{t}\right)_{t \in \mathbb{N}}\). By following the arguments given in Exercise 9.11, show that:

(i) the optimal demand of the risky asset by rational and noise traders is respectively given by

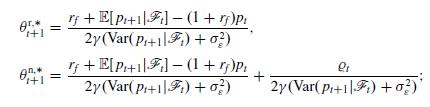
(ii) the steady-state equilibrium price process \(\left(p_{t}^{*}\right)_{t \in \mathbb{N}}\) of the risky asset satisfies

\[p_{t}^{*}=1+\frac{\mu_{t} \bar{\varrho}}{r_{f}}-\frac{2 \gamma}{r_{f}}\left(\sigma_{\varepsilon}^{2}+\frac{\mu^{2} \sigma_{\varrho}^{2}}{\left(1+r_{f}\right)^{2}}\right)+\frac{\mu_{t}\left(\varrho_{t}-\bar{\varrho}\right)}{1+r_{f}}\]

(iii) in correspondence of a steady-state equilibrium, the difference \(\mathbb{E}\left[\Delta R_{t+1}(\mu)\right]\) in the expected optimal return between the noise and the rational traders is given by

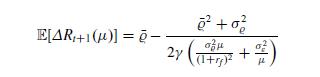
if \(\mu>0\) and \(\mathbb{E}\left[\Delta R_{t+1}(\mu)\right]=\bar{\varrho}\) if \(\mu=0\), for all \(t \in \mathbb{N}\).

Transcribed Image Text:

H+I rf+E[P+1] (1+r)pt 2y (Var(P+1)+02) 8= 1+1 +P+1(1+r)Pt 2y (Var(Pr+1)+02) et + 2y (Var(P+1) +)'