In the classical mean–variance portfolio optimization model, we use variance/standard deviation as a risk measure, but an alternative is mean absolute deviation (MAD), which is defined as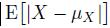 

, for a random variable X with expected value X. In other words, we get rid of the sign of deviations by taking their absolute value, rather than by squaring them. This may be more robust to outliers and leads to an LP, rather than a QP model.
We need an optimization model to minimize MAD in terms of monetary wealth (not return), with a constraint on a target expected wealth at the end of the holding horizon, while keeping transaction costs under control. We consider a single holding horizon from t = 0 to t = T, so that the model is static, rather than dynamic. We have the following information, for a set of N stock shares in which we may invest:
Current holding of each stock (number of stock shares we hold now, before rebalancing the portfolio at time t = 0)
Current price of each stock share at time t = 0 A set of M equally likely price scenarios for stock share prices at the end t = T of the holding horizon Expected wealth that we wish to achieve at time t = T (a minimum desired target)
In the objective function, we consider only MAD (the selected risk measure), but we also have a budget (upper bound) constraint on transaction costs, in order to limit the cost of trading. Let us assume that we may reduce transaction costs by trading with a broker that accepts to buy/sell only multiples of a basic lot of shares. For instance, if the basic lot is 1000, the broker will buy/sell 1000, 2000, 3000, : : :, stock shares. For each lot (of 1000 shares in the example), there is a fixed transaction cost. We can also buy or sell an arbitrary number of stock shares using a standard trading platform, where we incur a proportional cost for each trade (buy/sell), given by a percentage of the amount traded for each stock share (e.g, 0:5% on the total value of the shares we buy/sell). We are free to use any mix of broker/platform we want, as the only limit is on the total transaction cost. The model must be in MILP form.

Transcribed Image Text:

|E[|X-PX|]