Let us consider the PDE with terminal condition In order to apply the representation theorem, we observe
Question:
Let us consider the PDE
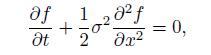
with terminal condition
![]()
In order to apply the representation theorem, we observe that \(r=0\), \((x t)=\), and 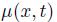 , so that the underlying stochastic process boils down to a martingale described by
, so that the underlying stochastic process boils down to a martingale described by
![]()
Therefore, conditional on \(X(t)=x\), integration over the time interval \(\left[\begin{array}{ll}t, & T\end{array}\right]\) yields
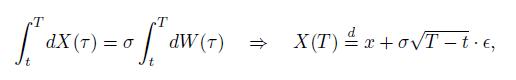
where ![]() . Therefore,
. Therefore,
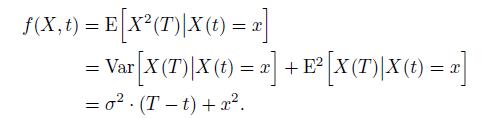
It is easy to check that this function satisfies the PDE and the terminal condition.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

An Introduction To Financial Markets A Quantitative Approach
ISBN: 9781118014776
1st Edition
Authors: Paolo Brandimarte
Question Posted:





