Let us consider the pure binary problem:

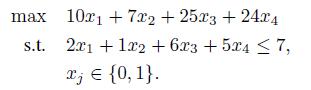
This kind of model is known as knapsack problem. We have a set of items, with given weight and value. We want to find a subset of items with maximum value, without exceeding the weight capacity of the knapsack. The problem can be considered as a simple version of a capital budgeting problem, where investments are indivisible and we must select the best subset, subject to a single resource budget. If we relax the integrality condition to  and solve the correspondingLP, we obtain

with objective value 36.2. This objective value is an upper bound on the optimal value. The solution is easy to interpret in the light of a possible greedy heuristic. We would like to choose items with a large value, but this must be traded off against the resource consumption.

Thus, we may compute a priority pj for each item, by taking ratios of value and weight:

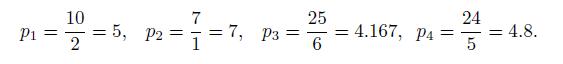
So, we may select the highest-priority items 2 and 1, but then only 80% of item 4 can be included. The actual solution we find includes items 2 and 1, providing a rather low value, 17, which is very far from the upper bound 36.2 and leaves a lot of budget unused. This rule does not guarantee optimality. In fact, it is easy to see that we are better off by selecting items 1 and 4, as this choice uses all of the budget and has value 34. Since the upper bound is 36.2, and all of the problem data are integer, we are sure that there is no way to find a solution with profit larger than 36. However, we cannot rule out the existence of a solution with a value larger than 34, yet, and we wonder whether the solution  is really optimal.To generate some additional cuts, let us observe that items 1 and 3 cannot be both selected, as their total weight is 8, larger than the budget. The same applies to items 1, 2, and 4. Hence we may add the cuts

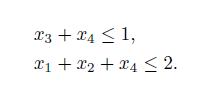
They are obviously redundant in the discrete domain, but they are not in the continuous relaxation. This kind of cut is called a cover cut.
By adding these two cover cuts, the LP relaxation yields a stronger bound, 34:66667 is optimal.

Transcribed Image Text:

max 10x1 +7x2 + 25x3 + 24x4 s.t. 2x11x2+6x3+5x4 <7, x; = {0, 1}.