Say that we want to "compute" the stochastic integral

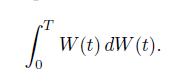
Analogy with ordinary calculus would suggest using the chain rule for the differentiation of composite functions, in order to obtain a differential that can be integrated directly. Specifically, we might guess that

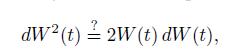
where we use \(\stackrel{?}{=}\) again to underline that we are just making guesses. This in turn would suggest that

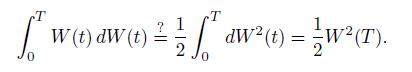
Unfortunately, this cannot be the correct answer, as it contradicts our previous findings. We have just seen that the expected value of an integral of this kind is zero, but

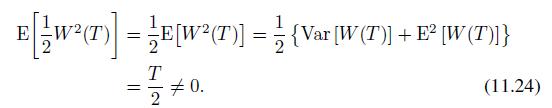
We see that the two expected values do not match at all, and there must be something wrong somewhere.

Transcribed Image Text:

T W (t) dW (t).