Consider a set of (m) assets, whose prices are modeled by stochastic processes , described by stochastic
Question:
Consider a set of \(m\) assets, whose prices are modeled by stochastic processes 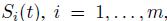 , described by stochastic differential equations like (11.18). Let us assume that we pursue a portfolio strategy represented by functions
, described by stochastic differential equations like (11.18). Let us assume that we pursue a portfolio strategy represented by functions  , which give the number of stock shares of each asset
, which give the number of stock shares of each asset 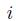 that we hold at time t. But which functions make sense? An obvious requirement is that functions
that we hold at time t. But which functions make sense? An obvious requirement is that functions  should not be anticipative:
should not be anticipative: 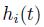 may depend on all the history so far, over the interval
may depend on all the history so far, over the interval 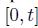 , but clairvoyance should be ruled out. Furthermore, we should think of
, but clairvoyance should be ruled out. Furthermore, we should think of 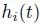 as the number of shares we hold over a time interval of the form
as the number of shares we hold over a time interval of the form 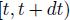 . Note that the interval is half-closed, to point out that we make a decision and rebalance the portfolio at time
. Note that the interval is half-closed, to point out that we make a decision and rebalance the portfolio at time  ; then, we keep the portfolio constant for a while and, at time \(t+t\), we will observe the result and make a new decision.
; then, we keep the portfolio constant for a while and, at time \(t+t\), we will observe the result and make a new decision.
Now, assume that we are endowed with an initial wealth that we have to allocate among the m assets. The initial portfolio value, depending on the portfolio strategy represented by the functions 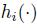 ,
,
is
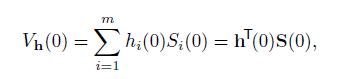

Step by Step Answer:

An Introduction To Financial Markets A Quantitative Approach
ISBN: 9781118014776
1st Edition
Authors: Paolo Brandimarte





