Suppose that we want to find the price of a vanilla European-style call with \(S_{0}=K=50, r=01,=04\), and \(T=\frac{5}{12}\) (time-to-maturity is five months). We must first set up the lattice parameters. Suppose that each time step is one month. Then,

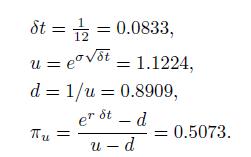
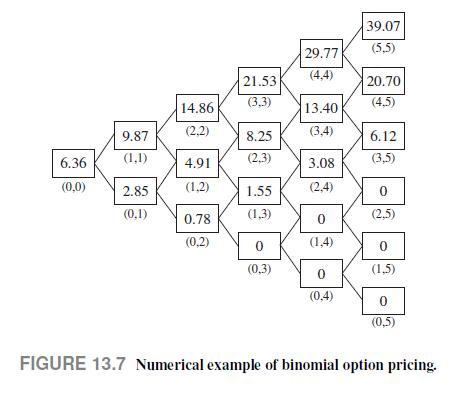
Figure 13.7 shows the resulting lattices for the stock price and the option value. To see how the lattice for the stock price is built, at node (ll) we have

which is the same as \(S_{35}=S_{0} u^{3} d^{2}\). The lattice of option values is initialized with the option payoffs. So, for instance,

The option value at the uppermost node in the second-to-last time layer, \(f_{44}\), depends on the option values \(f_{55}\) and \(f_{45}\), and is obtained as follows:

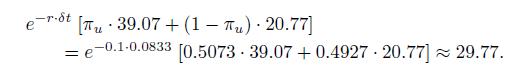
By going backward recursively, we find that the estimated option price is about 6.36. Later, in Example 13.6, we will see that the exact option price is 6.1165 . Hence, the approximation we have found is not bad at all, considering that we have used a very crude discretization, where each time step is one month. In practice, something like 1000 steps is needed to find a satisfactory approximation.

Data From Fig 13.7

Data From Example 13.6

Transcribed Image Text:

St == 0.0833, u = est = 1.1224, d=1/u 0.8909, er St - d u-d = 0.5073.