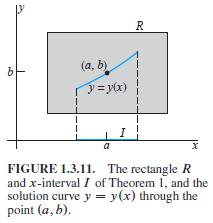
A more detailed version of Theorem 1 says that, if the function f (x, y) is continuous near the point (a, b), then at least one solution of the differential equation y' = f (x, y) exists on some open interval I containing the point x = a and, moreover, that if in addition the partial derivative ∂f /∂y is continuous near (a, b), then this solution is unique on some (perhaps smaller) interval J . In Problems 11 through 20, determine whether existence of at least one solution of the given initial value problem is thereby guaranteed and, if so, whether uniqueness of that solution is guaranteed.

Theorem 1

Figure 1.3.11

Transcribed Image Text:

dy dx = /x-y; y(2)=1