A second-order Euler equation is one of the form

where a, b, c are constants.

(a) Show that if x > 0, then the substitution v = ln x transforms Eq. (22) into the constant- coefficient linear equation

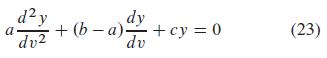
with independent variable v.

(b) If the roots r₁ and r₂ of the characteristic equation of Eq. (23) are real and distinct, conclude that a general solution of the Euler equation in (22) is y(x) = c₁x^r1 + c₂x^r2.

axy" + bxy' + cy=0 (22)