Example 4 dealt with the case 4h > kM² in the equation dx/dt = kx (M - x) - h that describes constant-rate harvesting of a logistic population. Problems 26 and 27 deal with the other cases.

If 4h > kM², show that x(t) = 0 after a finite period of time, so the lake is fished out (whatever the initial population). Then solve explicitly by separation of variables.] The results of this and the previous problem (together with Example 4) show that h = 1/4 kM² is a critical harvesting rate for a logistic population. At any lesser harvesting rate the population approaches a limiting population N that is less than M (why?), whereas at any greater harvesting rate the population reaches extinction.

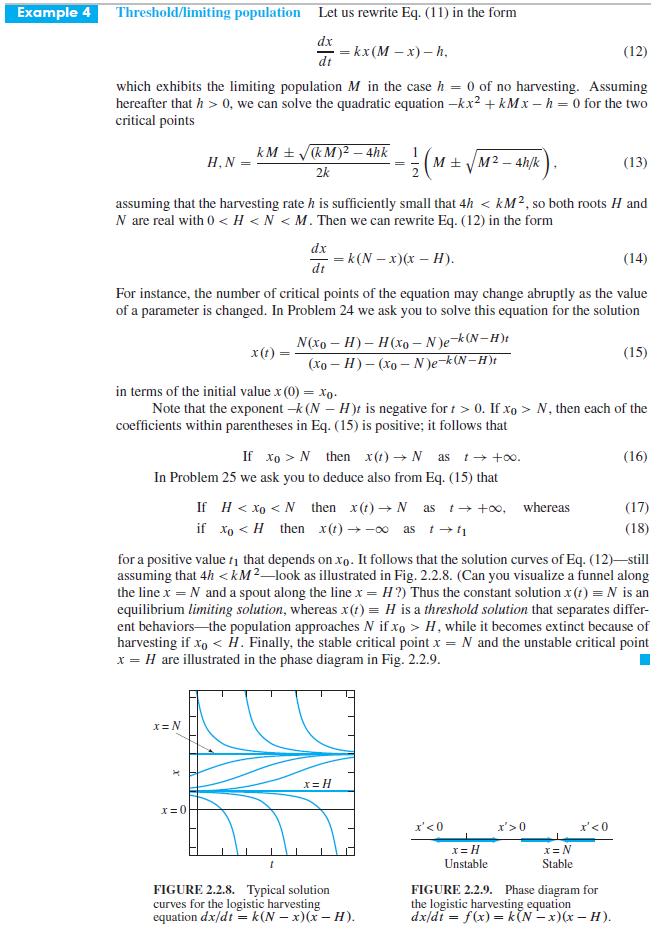
Transcribed Image Text:

Example 4 Threshold/limiting population (12) = which exhibits the limiting population M in the case h 0 of no harvesting. Assuming hereafter that h> 0, we can solve the quadratic equation -kx² +kMx-h=0 for the two critical points H, N Let us rewrite Eq. (11) in the form dx dt kM ± √(KM)² - 4hk 2k x=N = kx (M-x) - h. x=0 assuming that the harvesting rate h is sufficiently small that 4h < KM2, so both roots H and N are real with 0 N then x(1)→ N as t→ +∞0. In Problem 25 we ask you to deduce also from Eq. (15) that N(xo-H)-H(xo-N)e-k(N-H)t (xo-H)-(xo-N)e-k(N-H)t x(t) in terms of the initial value x (0) = xo. Note that the exponent -k (NH)t is negative for t > 0. If xo> N, then each of the coefficients within parentheses in Eq. (15) is positive; it follows that If H < xo < N then x(t) → N as t→ +∞o, whereas if xo H, while it becomes extinct because of harvesting if xo < H. Finally, the stable critical point x = N and the unstable critical point x = H are illustrated in the phase diagram in Fig. 2.2.9. x'<0 x=H Unstable (13) x'>0 x = N Stable x'<0 (15) FIGURE 2.2.9. Phase diagram for the logistic harvesting equation dx/dt = f(x) = k(N-x)(x-H). (16) (17) (18)