Given a mass m, a dashpot constant c, and a spring constant k, Theorem 2 of Section

Question:

Given a mass m, a dashpot constant c, and a spring constant k, Theorem 2 of Section 5.1 implies that the equation

has a unique solution for t ≧ 0 satisfying given initial conditions x (0) = x₀, x'(0) = v₀. Thus the future motion of an ideal mass-spring-dashpot system is completely determined by the differential equation and the initial conditions. Of course in a real physical system it is impossible to measure the parameters m, c, and k precisely. Problems 35 through 38 explore the resulting uncertainty in predicting the future behavior of a physical system.

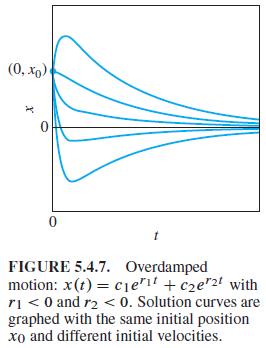
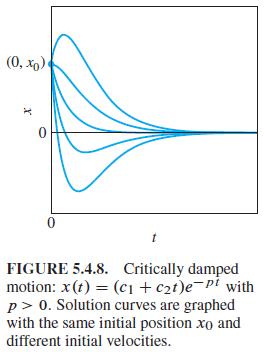
Whereas the graphs of x₁ (t) and x₂ (t) resemble those shown in Figs. 5.4.7 and 5.4.8, the graph of x₃ (t) exhibits damped oscillations like those illustrated in Fig. 5.4.9, but with a very long pseudoperiod. Nevertheless, show that for each fixed t > 0 it is true that