Problems 23 through 25 deal with the case ∈ = 1, so that the system in (6) takes the form

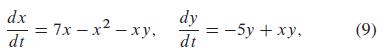
and these problems imply that the three critical points (0,0), (7,0), and (5,2) of the system in (9) are as shown in Fig. 9.3.18 -with saddle points at the origin and on the positive x-axis and with a spiral sink at (5,2). In each problem use a graphing calculator or computer system to construct a phase plane portrait for the linearization at the indicated critical point. Do your local portraits look consistent with Fig. 9.3.18?

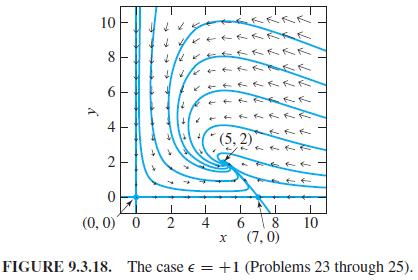
Show that the linearization of (9) at (5,2) is u' = -5u - 5v, v' = 2u. Then show that the coefficient matrix of this linear system has complex conjugate eigenvalues λ₁, λ₂ = 1/2 (-5 ± i √15) with negative real part. Hence (5, 2) is a spiral sink for the system in (9).

dx dt = 7x-x-xy, dy dt 5y+xy, (9)