Question: The phase portraits in Problems 17 through 28 correspond to linear systems of the form x' = Ax in which the matrix A has two

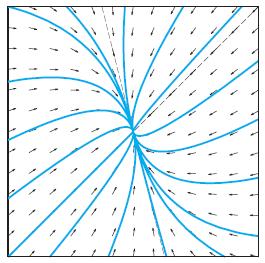
The phase portraits in Problems 17 through 28 correspond to linear systems of the form x' = Ax in which the matrix A has two linearly independent eigenvectors. Determine the nature of the eigenvalues and eigenvectors of each system. For example, you may discern that the system has pure imaginary eigenvalues, or that it has real eigenvalues of opposite sign; that an eigenvector associated with the positive eigenvalue is roughly [2 -1]T , etc.

Zal

Zal

Step by Step Solution

★★★★★

3.43 Rating (153 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

The phase portrait you have provided corresponds to a type of critical point known as an unstable st... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related First Course Differential Equations Questions!

Q:

A British food distribution conglomerate purchased a Canadian food store chain for $75 million (U.S.) three years ago. There was a net loss of $10 million at the end of year 1 of ownership. Net cash...

Q:

The phase portraits in Problems 17 through 28 correspond to linear systems of the form x' = Ax in which the matrix A has two linearly independent eigenvectors. Determine the nature of the eigenvalues...

Q:

The phase portraits in Problems 17 through 28 correspond to linear systems of the form x' = Ax in which the matrix A has two linearly independent eigenvectors. Determine the nature of the eigenvalues...

Q:

The phase portraits in Problems 17 through 28 correspond to linear systems of the form x' = Ax in which the matrix A has two linearly independent eigenvectors. Determine the nature of the eigenvalues...

Q:

The phase portraits in Problems 17 through 28 correspond to linear systems of the form x' = Ax in which the matrix A has two linearly independent eigenvectors. Determine the nature of the eigenvalues...

Q:

The phase portraits in Problems 17 through 28 correspond to linear systems of the form x' = Ax in which the matrix A has two linearly independent eigenvectors. Determine the nature of the eigenvalues...

Q:

The phase portraits in Problems 17 through 28 correspond to linear systems of the form x' = Ax in which the matrix A has two linearly independent eigenvectors. Determine the nature of the eigenvalues...

Q:

The phase portraits in Problems 17 through 28 correspond to linear systems of the form x' = Ax in which the matrix A has two linearly independent eigenvectors. Determine the nature of the eigenvalues...

Q:

The phase portraits in Problems 17 through 28 correspond to linear systems of the form x' = Ax in which the matrix A has two linearly independent eigenvectors. Determine the nature of the eigenvalues...

Q:

The phase portraits in Problems 17 through 28 correspond to linear systems of the form x' = Ax in which the matrix A has two linearly independent eigenvectors. Determine the nature of the eigenvalues...

Q:

The phase portraits in Problems 17 through 28 correspond to linear systems of the form x' = Ax in which the matrix A has two linearly independent eigenvectors. Determine the nature of the eigenvalues...

Q:

A furniture maker has 6 wood panels and 30 hours of free time: He sells two types of cabinets made from these panels. The first cabinet requires 2 pieces of panels and 7 hors. The second cabinet...

Q:

Rainman Corporation is considering the acquisition of Largo Company through the acquisition of Largos common stock. Rainman Corporation will issue 20,000 shares of its $5 par common stock, with a...