Consider steady, laminar, fully developed, two dimensional Poiseuille flow—flow between two infinite parallel plates separated by distance h, with both the top plate and bottom plate stationary, and a forced pressure gradient dP/dx driving the flow as illustrated in Fig. P7–95. (dP/dx is constant and negative.) The flow is steady, incompressible, and two-dimensional in the xy-plane. The flow is also fully developed, meaning that the velocity profile does not change with downstream distance x. Because of the fully developed nature of the flow, there are no inertial effects and density does not enter the problem. It turns out that u, the velocity component in the x-direction, is a function of distance h, pressure gradient dP/dx, fluid viscosity μ, and vertical coordinate y. Perform a dimensional analysis (showing all your work), and generate a dimensionless relationship between the given variables.

FIGURE P7–95

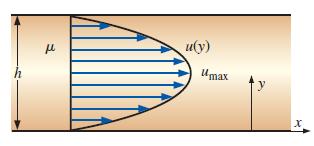
u(y) Umax x