For the fluid falling between two parallel vertical walls (Prob. 9–91), generate an expression for the volume flow rate per unit width (V̇/L) as a function of ρ, μ, h, and g. Compare your result to that of the same fluid falling along one vertical wall with a free surface replacing the second wall (Example 9–17), all else being equal. Discuss the differences and provide a physical explanation.

Data from Problem 9-91

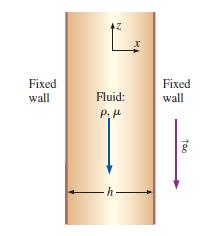
Consider steady, incompressible, parallel, laminar flow of a viscous fluid falling between two infinite vertical walls (Fig. P9–91). The distance between the walls is h, and gravityacts in the negative z-direction (downward in the figure). There is no applied (forced) pressure driving the flow—the fluid fall by gravity alone. The pressure is constant everywhere in the flow field. Calculate the velocity field and sketch the velocity profile using appropriate nondimensionalized variables.

FIGURE P9–91

Data from Example 9-17

Consider steady, incompressible, parallel, laminar flow of a film of oil falling slowly down an infinite vertical wall (Fig. 9–68). The oil film thickness is h, and gravity acts in the negative z-direction (downward in Fig. 9–68). There is no applied (forced) pressure driving the flow—the oil falls by gravity alone. Calculate the velocity and pressure fields in the oil film and sketch the normalized velocity profile. You may neglect changes in the hydrostatic pressure of the surrounding air.

FIGURE 9–68

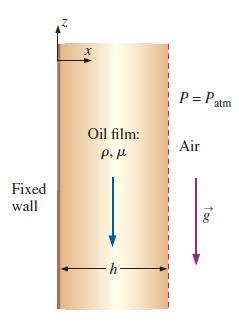
Fixed wall X Oil film: P l -h- 1 P= Patm Air Too