For the falling oil film of Prob. 9–113, calculate the volume flow rate per unit width of oil falling down the wall (V̇/L) as a function of wall speed V and the other parameters in the problem. Calculate the wall speed required such that there is no net volume flow of oil either up or down. Give your answer for V in terms of the other parameters in the problem, namely, ρ, μ, h, and g. Calculate V for zero volume flow rate for an oil film of thickness 4.12 mm with ρ = 888 kg/m³ and μ = 0.801 kg/m·s.

Data from Problem 113

Repeat Example 9–17, except for the case in which the wall is moving upward at speed V. As a check, make sure that your result agrees with that of Example 9–17 when V = 0. Nondimensionalize your velocity profile equation using the same normalization as in Example 9–17, and show that a Froude number and a Reynolds number emerge. Plot the profile w* versus x* for cases in which Fr = 0.5 and Re = 0.5, 1.0, and 5.0. Discuss.

Data from Example 9-17

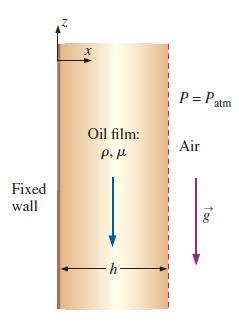
Consider steady, incompressible, parallel, laminar flow of a film of oil falling slowly down an infinite vertical wall (Fig. 9–68). The oil film thickness is h, and gravity acts in the negative z-direction (downward in Fig. 9–68). There is no applied (forced) pressure driving the flow—the oil falls by gravity alone. Calculate the velocity and pressure fields in the oil film and sketch the normalized velocity profile. You may neglect changes in the hydrostatic pressure of the surrounding air.

FIGURE 9–68

Transcribed Image Text:

Fixed wall X Oil film: P₂ μl -h- 1 P= Patm Air Too