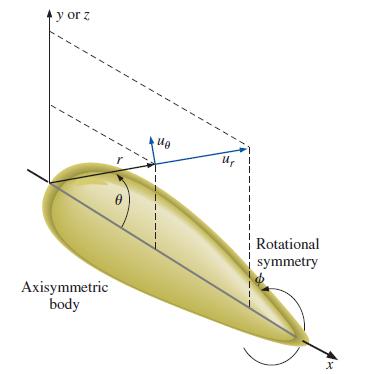
In this chapter, we describe axisymmetric irrotational flow in terms of cylindrical coordinates r and z and velocity components u_r and u_z. An alternative description of axisymmetric flow arises if we use spherical polar coordinates and set the x-axis as the axis of symmetry. The two relevant directional components are now r and θ, and their corresponding velocity components are u_r and uθ. In this coordinate system, radial location r is the distance from the origin, and polar angle θ is the angle of inclination between the radial vector and the axis of rotational symmetry (the x-axis), as sketched in Fig. P10–62; a slice defining the rθ-plane is shown. This is a type of two dimensional flow because there are only two independent spatial variables, r and θ. In other words, a solution of the velocity and pressure fields in any rθ-plane is sufficient to characterize the entire region of axisymmetric irrotational flow. Write the Laplace equation for Φ in spherical polar coordinates, valid in regions of axisymmetric irrotational flow.

FIGURE P10–62

Transcribed Image Text:

y or z Axisymmetric body 1 3 1 ve 7 1 1 U₂ Rotational symmetry X