Consider a photon emitted by an atom at rest on the surface of a static star with mass M and radius R. Analyze the photon’s motion in the Schwarzschild coordinate system of the star’s exterior, r ≥ R > 2M. In particular, compute the “gravitational redshift” of the photon by the following steps.

(a) Since the emitting atom is nearly an ideal clock, it gives the emitted photon nearly the same frequency ν_em, as measured in the emitting atom’s proper reference frame (as it would give were it in an Earth laboratory or floating in free space). Thus the proper reference frame of the emitting atom is central to a discussion of the photon’s properties and behavior. Show that the orthonormal basis vectors of that proper reference frame are

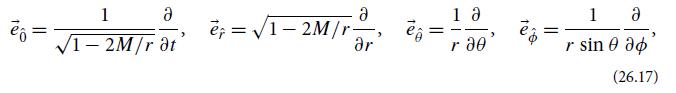
with r = R (the star’s radius).
(b) Explain why the photon’s energy as measured in the emitter’s proper reference frame is

(c) Show that the quantity ε_∞ ≡ −p_t = −p(vector) · ∂/∂t is conserved as the photon travels outward from the emitting atom to an observer at very large radius, which we idealize as r = ∞.

(d) Show that

and thence that

and that therefore the photon is redshifted by an amount

Here λ_rec is the wavelength that the photon’s spectral line exhibits at the receiver, and λ_em is the wavelength that the emitting kind of atom would produce in an Earth laboratory. Note that for a nearly Newtonian star (i.e., one with R ≫ M), this redshift becomes ≈ M/R = GM/Rc².

(e) Evaluate this redshift for Earth, for the Sun, and for a 1.4-solar-mass, 10-km radius neutron star.

10 = 1 /1-2M/rat e; =1 - 2M/r- ar > = 12 1 r sin 0 (26.17)