Bruno Bertotti (1959) and Ivor Robinson (1959) independently solved the Einstein field equation to obtain the following
Question:
Bruno Bertotti (1959) and Ivor Robinson (1959) independently solved the Einstein field equation to obtain the following metric for a universe endowed with a uniform magnetic field:
![]()
Here
![]()
If one computes the Einstein tensor from the metric coefficients of the line element (26.13) and equates it to 8π times a stress-energy tensor, one finds a stress energy tensor that is precisely the same as for an electromagnetic field [Eqs. (2.75) and (2.80)] lifted, unchanged, into general relativity. The electromagnetic field is one that, as measured in the local Lorentz frame of an observer with fixed {z, θ, ∅} (a “static” observer), has vanishing electric field and has a magnetic field directed along ∂/∂z with magnitude independent of where the observer is located in spacetime. In this sense, the spacetime metric (26.13) is that of a homogeneous magnetic universe. Discuss the geometry of this universe and the nature of the coordinates {t , z, θ, ∅}. More specifically, do the following.
(a) Which coordinate increases in a timelike direction and which coordinates in spacelike directions?
(b) Is this universe spherically symmetric?
(c) Is this universe cylindrically symmetric?
(d) Is this universe asymptotically flat?
(e) How does the geometry of this universe change as t ranges from 0 to π?
(f) Give as complete a characterization as you can of the coordinates {t , z, θ , ∅}
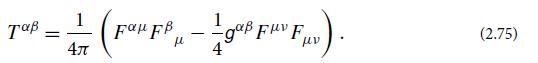

Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





