Repeat Prob. 9–96, but let the inner cylinder be stationary and the outer cylinder rotate at angular velocity ω_o. Generate an exact solution for u_θ(r) using the step-by-step procedure discussed in this chapter.

Data from Problem 96

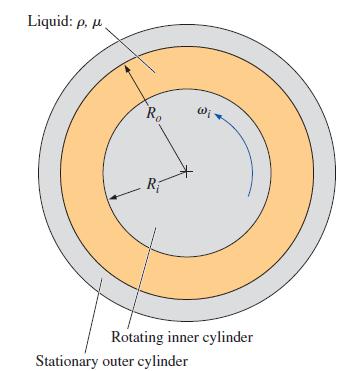
An incompressible Newtonian liquid is confined between two concentric circular cylinders of infinite length— a solid inner cylinder of radius R_i and a hollow, stationary outer cylinder of radius R_o (Fig. P9–96; the z-axis is out of the page). The inner cylinder rotates at angular velocity ω_i. The flow is steady, laminar, and two-dimensional in the r_θ-plane. The flow is also rotationally symmetric, meaning that nothing is a function of coordinate θ (u_θ and P are functions of radius r only). The flow is also circular, meaning that velocity component u_r = 0 everywhere. Generate an exact expression for velocity component u_θ as a function of radius r and the other parameters in the problem. You may ignore gravity.

FIGURE P9–96

Transcribed Image Text:

Liquid: p. p. Ro Wi Rotating inner cylinder Stationary outer cylinder