Repeat Prob. 996 for the more general case. Namely, let the inner cylinder rotate at angular velocity i and let the outer cylinder rotate

Repeat Prob. 9–96 for the more general case. Namely, let the inner cylinder rotate at angular velocity ω_i and let the outer cylinder rotate at angular velocity ω_o. All else is the same as Prob. 9–96. Generate an exact expression for velocity component u_θ as a function of radius r and the other parameters in the problem. Verify that when ω_o = 0 your result simplifies to that of Prob. 9–96.

Data from Problem 9-96

An incompressible Newtonian liquid is confined between two concentric circular cylinders of infinite length— a solid inner cylinder of radius R_i and a hollow, stationary outer cylinder of radius R_o (Fig. P9–96; the z-axis is out of the page). The inner cylinder rotates at angular velocity ω_i. The flow is steady, laminar, and two-dimensional in the r_θ-plane. The flow is also rotationally symmetric, meaning that nothing is a function of coordinate θ (u_θ and P are functions of radius r only). The flow is also circular, meaning that velocity component u_r = 0 everywhere. Generate an exact expression for velocity component u_θ as a function of radius r and the other parameters in the problem. You may ignore gravity.

FIGURE P9–96

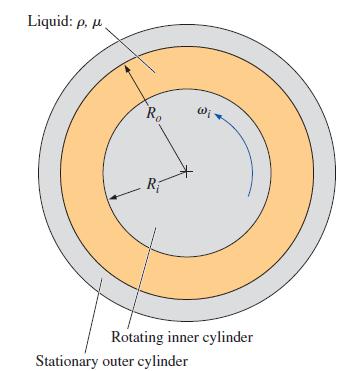
Liquid: p. p. Ro Wi Rotating inner cylinder Stationary outer cylinder