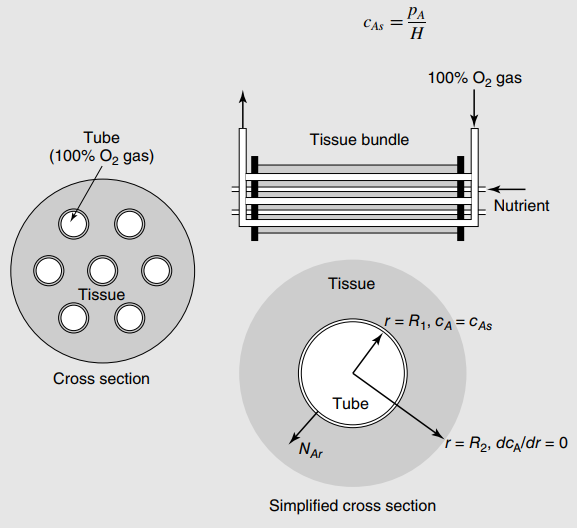
Recall from example 3, Chapter 25, that the differential model for the radial concentration profile of dissolved oxygen within one cylindrical engineered tissue bundle (Figure 25.8) is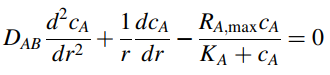

with boundary conditions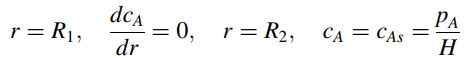

Often, K_A is very small relative to c_A so that the homogeneous reaction term approaches a zero-order process that is not dependent on concentration:

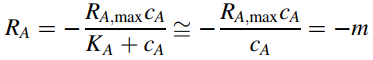
so that

where m is the metabolic respiration rate of the tissue. In the present process, in = 0.25 mole/m³ · h at 25^°C, and R₁ and R₂ are equal to 0.25 cm and 0.75 cm, respectively. Pure O₂ gas at 1.0 atm flows through the tube of length 15 cm. The mass- transfer resistance due to the thin-walled tube is neglected, and the Henry€™s law constant for dissolution of O₂ in the tissue is 0.78 atm · m³/mole at 25^°C. The diffusion coefficient of oxygen in water is 2.1 · 10^-5 cm²/s at 25^°C, which approximates the diffusivity of oxygen dissolved in the tissue. 

a. Develop a model, in final integrated form, to predict the concentration profile c_A(r), and then plot out the concentration profile. Note that for diffusion with zero-order homo geneous chemical reaction, there will be a critical radius, R_c, where the dissolved oxygen concentration goes to zero. Therefore, if R_c 2, then c_A (r) = 0 from r = R_c to r = R₂.

b. Using this model and the process input parameter detailed above, determine R_c. Then, plot of the concentration profile from c_A(r) from r = R₁ to r = R_c. 

c. Develop a model, in final algebraic form, to predict W_A, total oxygen transfer rate through one tube. From the process input parameters given in the problem statement, calculate W_A.

Figure 25.8

d'cA DAB 1 dca RA,maxCA KA + CA 0 = r dr dr? PA r = R1, dca = 0, dr r = R2, CA = CAS