Transform the operator to cylindrical coordinates (r, θ, z), using the results of Problems 1.7 and 1.9. Data From Problem 1.7 Show that the unit

Transform the operator ˆ‡ to cylindrical coordinates (r, θ, z), using the results of Problems 1.7 and 1.9.

Data From Problem 1.7

Show that the unit vectors e_r and e_θ in a cylindrical coordinate system are related to the unit vectors e_x and e_y by

e_r = e_x cos θ + e_y sin θ

and

e_θ = -e_x sin θ + e_y cos θ

Data From Problem 1.9

Using the geometric relations given below and the chain rule for differentiation, show that

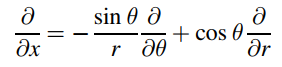
and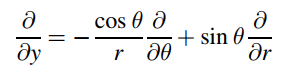

when r² = x² + y² and tanθ = y/x.

sin 0 + cos 0. r r 0 cos 0 a r 0 + sin 0 r ||