Using the integral relations from Problem 19.17, and assuming the velocity and temperature profiles of the form
Question:
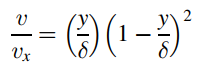
and
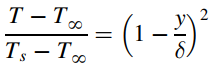
where δ is the thickness of both the hydrodynamic and thermal boundary layers, show that the solution in terms of δ and vx from each integral equation reduce to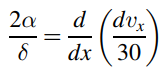 and
and
Next, assuming that both δ and vx vary with x according to
δ = Axα and vx = Bxb
show that the resulting expression for d becomes
δ/x = 3.94 Pr-1/2 (Pr + 0.953)1/4 Grx-1/4
and that the local Nusselt number is
Nux = 0.508 Pr-1/2 (Pr + 0.953)-1/4 Grx1/4
Data From Problem 19.17
Show that, for the case of natural convection adjacent to a plane vertical wall, the appropriate integral equations for the hydrodynamic and thermal boundary layers are  and
and
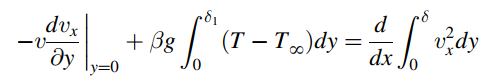
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Fundamentals Of Momentum Heat And Mass Transfer
ISBN: 9781118947463
6th Edition
Authors: James Welty, Gregory L. Rorrer, David G. Foster
Question Posted:





