A nicotine patch is designed to deliver \(24 \mathrm{mg}\) of nicotine over a \(24 \mathrm{hr}\) period. The patch is \(5 \mathrm{~cm}\) in diameter as shown in Figure P4.35. The steady-state nicotine concentration in the blood is designed to be \(1 \mu \mathrm{g} /\) liter. Assuming the nicotine must pass through the skin, a layer of fat just beneath the skin, and finally into the blood, what is the concentration at the patch-skin interface? The partition coefficient between the patch and skin is \(K_{e q}=\frac{c_{\text {patch }}}{c_{\text {skin }}}=10\) and between the fat and blood is 1000 . All other partition coefficients are 1.

The diffusivities of nicotine in the skin and fat layer are: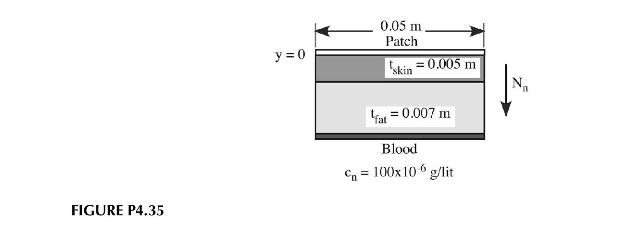

Data: \(D_{n s}=1.0 \times 10^{-10} \mathrm{~m}^{2} / \mathrm{s} \quad D_{n f}=1.0 \times 10^{-9} \mathrm{~m}^{2} / \mathrm{s}\)

Transcribed Image Text:

y=0 0.05 m Patch skin=0.005 m FIGURE P4.35 fat = 0.007 m Blood C = 100x100 g/lit