Assume that the analogy discussed in Problem 11.31 holds. That means that we would have an overall mass transfer coefficient that serves as the replacement for the overall heat transfer coefficient. How might one go about defining this overall coefficient and what would the resistance network look like? Instead of a diffusion coefficient through the membrane, we use a permeability defined by \(\mathrm{K}\).

Problem 11.31

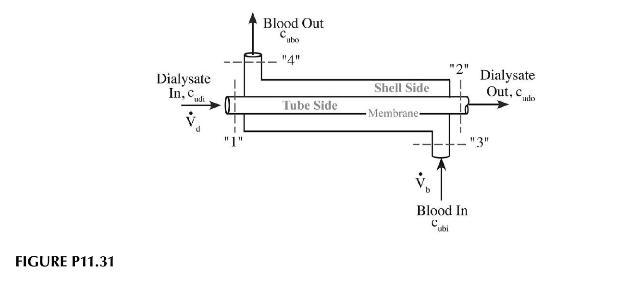
The analog of a shell-and-tube heat exchanger, or our double-pipe configuration, is a membrane system used for hemodialysis. Here, instead of a solid pipe wall passing heat, we have a porous membrane system that allows impurities like urea to pass through. The amount of mass transfer is insufficient to alter the overall flow rates of the shell side or tube-side fluids, i.e., we are using dilute solutions. The system uses counterflow operation with blood passing through one side of the exchanger and dialysate fluid passing through on the opposite side as shown in Figure P11.31.

Assuming the analogy between the heat exchanger and this mass exchanger holds, what would be the design equation and the log-mean driving force?

Transcribed Image Text:

FIGURE P11.31 Dialysate In, c udi V Blood Out C ubo "4" "2" Shell Side Dialysate Out, c indo Tube Side Membrane- Blood In Cubi "3"