Consider the example in Section 10.4 about mass transfer to a growing bubble. Calculate the mass transfer coefficient for that system. Does it increase or decrease over time? Why should this be so?

Transcribed Image Text:

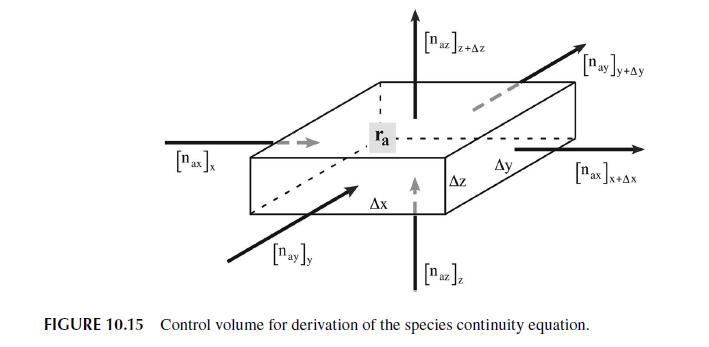
10.4 MASS TRANSPORT Though the overall mass may be conserved, individual species may accumulate in the system through convection, diffusion, or chemical reaction. In this section we will apply conservation of mass to an individual species within a fixed volume element in space and thereby derive the species continuity equation. Figure 10.15 shows the control volume we will use. We implicitly assume the system is a binary mixture of a and b. The balance equation considers convection in an out of the control volume, diffusion through the surfaces of the volume, generation of a species via reaction, and accumulation within the control volume. In Rate of a in by convection Rate of a in by diffusion Out Rate of a + Gen = Acc out by convection + Rate of a - + out by diffusion Net rate of a produced = Rate of a accumulated In - Out [nax (x)-nax (x+Ax)]AyAz +[nay (y) nay (y+ Ay)] AxAz +Gen = Acc (10.105) +[naz (2)-naz (z+Az)] ArAy+rAxAyAz = AxAyAz- t