Consider the mass transfer example concerning diffusion into a falling film shown in Figure P10.38. A new
Question:
Consider the mass transfer example concerning diffusion into a falling film shown in Figure P10.38. A new inventor claims that he can rig the device to operate such that the flux of \(a\) from the gas to the liquid is constant rather than the concentration at the interface being constant. He claims that this will provide a better mass transfer situation.
a. Rework the solution to this example assuming the mass flux at the interface is a constant, \(N_{a i}\).
b. How does the mass transfer coefficient behave as a function of position along the length of the plate?
c. For typical values of material properties, calculate an average mass transfer coefficient and determine what the flux would have to be to break even on this new process.
\[\begin{aligned}& D_{a b}=1 \times 10^{-10}\left(\mathrm{~m}^{2} / \mathrm{s}\right) \quad L=1(\mathrm{~m}) \quad \delta=100(\mu \mathrm{m}) \\& v=1 \times 10^{-6}\left(\mathrm{~m}^{2} / \mathrm{s}\right) \quad c_{a o}=10 \mathrm{~mol} / \mathrm{m}^{3}\end{aligned}\]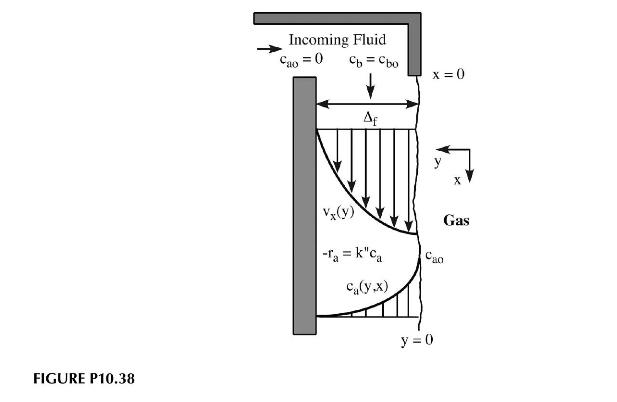
Step by Step Answer:






