Consider the flow formed by placing a source of strength, (q_{o}), a distance, (d), from an infinitely
Question:
Consider the flow formed by placing a source of strength, \(q_{o}\), a distance, \(d\), from an infinitely long wall as shown in Figure P9.18. The velocity potential for this incompressible and irrotational flow field is:
\[\phi=\frac{q_{o}}{4 \pi}\left\{\ln \left[(x-d)^{2}+y^{2}\right]+\ln \left[(x+d)^{2}+y^{2}\right]\right\}\]
a. Demonstrate that there is no flow through the wall.
b. How does the velocity vary along the length of the wall?
c. In 1738, Daniel Bernoulli showed that for an incompressible fluid exhibiting an irrotational flow field that
\[P+\frac{1}{2} ho v^{2}+ho g z=\text { constant } \quad \text { Bernoulli's equation }\]
Here \(z\) is the height of the fluid above some reference and \(v^{2}=v_{x}^{2}+v_{y}^{2}\). Using this result (we derive it in Chapter 11) and the fact that \(P=P_{o}\) far away from the source, determine the pressure distribution along the wall.
d. What does the stream function for this flow look like?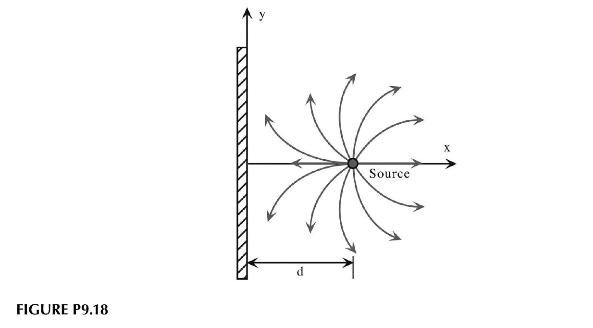
Step by Step Answer:






