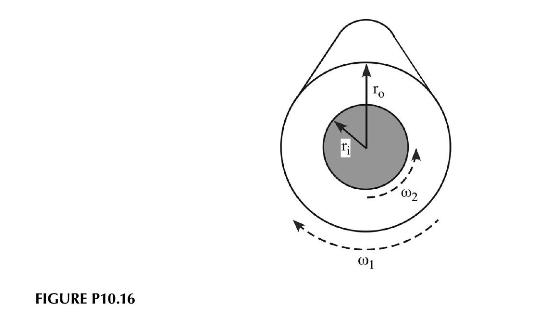
Consider the system shown in Figure P10.16 of two concentric rotating cylinders. The two cylinders each rotate at a constant but different angular velocity.

a. Determine the velocity profile \(v_{\theta}(r)\) between the cylinders and the pressure distribution in the radial direction \(P(r)\).

b. Determine a friction factor by calculating the force required to turn either of the two cylinders. Looking at the outer cylinder, we have:

\[F=\tau_{r \theta} A=C_{f}\left(\frac{1}{2} ho v_{o}^{2}\right) A\]

\(v_{o}\) is the linear velocity of the outer cylinder in \(\mathrm{m} / \mathrm{s}\).

Transcribed Image Text:

FIGURE P10.16 001 To