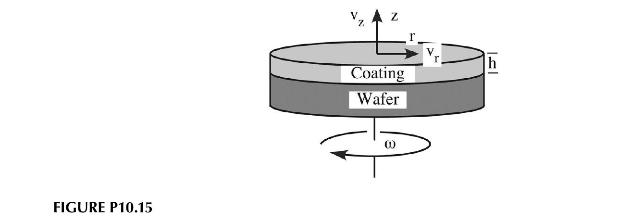
Consider the spin-coating process used to coat silicon wafers with photoresist, television picture tubes with phosphorescent layers, etc. (Figure P10.15). In all cases, the process is designed to produce a very thin, uniform coating by spinning a viscous, Newtonian, liquid onto a substrate. The process has angular symmetry, the rotation rate is constant, and since the film is thin, there are no real pressure gradients or fluid accelerations to speak of. The thin film also moves with the substrate as if it were a rigid body, \(v_{\theta} eq f(z)\).

a. Since we do not need to determine the pressure in the film, we need only determine \(v_{r}\) and \(v_{z}\). Show that the continuity and momentum equations reduce to:

\[-ho \frac{v_{\theta}^{2}}{r}=\mu \frac{d^{2} v_{r}}{d z^{2}} \quad \frac{1}{r} \frac{\partial}{\partial r}\left(r v_{r}\right)+\frac{\partial v_{z}}{\partial z}=0\]

\section*{Continuity}

\section*{Momentum}

b. What are the boundary conditions for this problem?

c. Solve the equations for \(v_{r}\) and \(v_{z}\).

d. The velocity, \(v_{z}\), at the film/air interface is just the change in film thickness with time. Use this to obtain a differential equation for \(h\), and integrate this equation to obtain the solution:

\[\frac{1}{2}\left(\frac{1}{h^{2}}+\frac{1}{h_{o}^{2}}\right)=\left(\frac{2 ho \omega^{2}}{3 \mu}\right) t\]

Transcribed Image Text:

FIGURE P10.15 Vz Z Coating Wafer h