Diffusion of dopants into solids under the application of an electric field often requires the introduction of a composition-dependent diffusivity to account for the phenomenon of "elastic drift" where the solid resists the introduction of additional atoms into its lattice by a kind of mechanical, or spring-like, force [3]. Following the discussion in Section 4.6.1, assume that we can express elastic drift using a linear expression for diffusivity as a function of concentration. Initial impression might suggest that the diffusivity should decrease with increasing dopant concentration. Show that this idea cannot work and that to actually increase the resistance, the diffusivity must increase with dopant concentration (i.e., we need a less steep profile at equilibrium). The total flux consists of two components, one due to diffusion and another due to drift within the electric field that can be written simply as a velocity times a concentration \(\left(f l u x=v_{\text {electric }} c\right.\) ).

Transcribed Image Text:

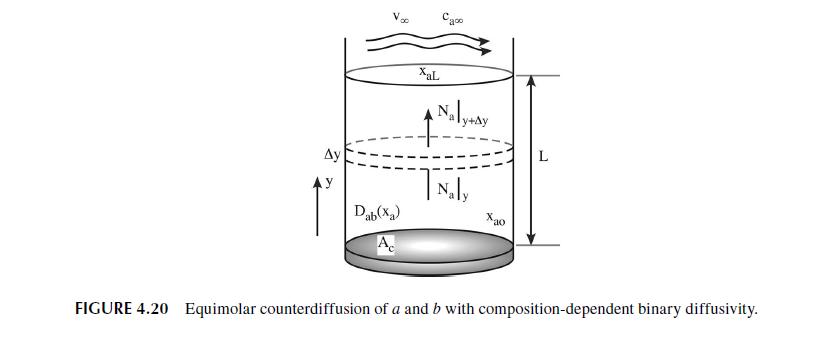
4.6.1 COMPOSITION DEPENDENT DIFFUSIVITY In this first example, we consider a common case where the diffusivity of a medium depends upon the composition of the medium and where the diffusion process itself is the agent that changes this composition. In Figure 4.20, we show a situation analogous to Figure 4.8 with the exception that we allow the diffusivity of species a to vary linearly with the amount of species a present in the solution. The situation is one where we will have equimolar counter-diffusion of species a and b. We analyze this situation in exactly the same manner we used when considering mass transfer with constant diffusivity. The starting point involves writing the balance equation (conservation of mass) over a small control volume of area, A., and width, Ay. In Ma(y) - - Out + Gen Acc = Ma (y+Ay) + 0 = 0 (4.130) Since, Ma = AcNa, dividing by AyA, and letting Ay 0 yields the differential equation stating that the molar flux is a constant throughout the system. dNa dy = 0 (4.131) We are interested in the mole fraction profile throughout the system and so we transform the dif- ferential equation by substituting for N using Fick's Law. Assuming equimolar counter-diffusion and an incompressible solution, dxa Na = -CDab dy (4.132)