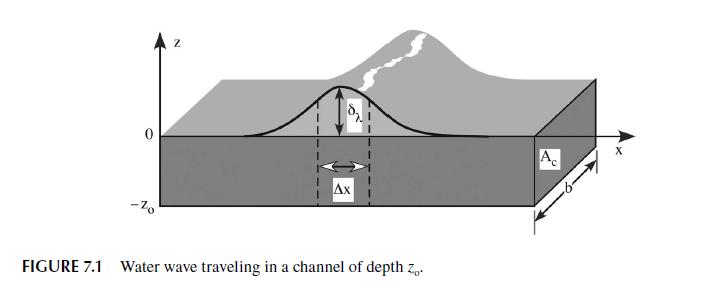
It is possible to consider the effect of small disturbing forces acting on water waves in canal of depth \(h\). Since the height of a wave is assumed to be very small, the only component of force that we need to consider is that component acting along the canal in the \(x\) direction. In essence, we add the force to the momentum equation before combining it with the continuity equation. Show that for an arbitrary force per unit mass, \(f(x)\), and a canal like that shown in Figure 7.1 in the text, the differential equation describing the amplitude of the wave is given by:

\[\left[\frac{g A_{c}}{b}\right] \frac{\partial^{2} \delta_{\lambda}}{\partial x^{2}}-\left[\frac{A_{c}}{b}\right] \frac{\partial f}{\partial x}=\frac{\partial^{2} \delta_{\lambda}}{\partial t^{2}}\]

Transcribed Image Text:

Z Ax -Zo FIGURE 7.1 Water wave traveling in a channel of depth Z- Ac