Consider a shallow lake on the equator and assume that the only tide-raising force is due to
Question:
Consider a shallow lake on the equator and assume that the only tide-raising force is due to the Moon. In Figure P7.9, \(O\) represents the center of the Earth. \(M\) is the point on the equator directly under the Moon. \(G\) represents \(0^{\circ}\) longitude at the equator, and \(P\) is the point we are interested in at \(\theta^{\circ}\) longitude. The Moon moves with a constant angular velocity, \(v_{\theta}\), so that at any time, \(t\), the angle between the Moon and \(G\), is \(v_{\theta} t+\phi\). The tide-raising force, per unit mass of water, at \(P\) is \(f=f_{o} \sin \left(v_{\theta} t+\phi+\theta\right)\).
a. Using the results of the previous problem, show that the differential equation describing the wave height can be written as:
\[\frac{\partial^{2} \delta_{\lambda}}{\partial t^{2}}=\left[\frac{c_{\lambda}^{2}}{r_{o}^{2}}\right] \frac{\partial^{2} \delta_{\lambda}}{\partial \theta^{2}}+\left[\frac{2 h_{o} f_{o}}{r_{o}}\right] \cos \left(v_{\theta} t+\phi+\theta\right)\]
where \(r_{o}\) is the radius of the Earth and \(h_{o}\) is the depth of the lake.
b. The solution can be obtained in two parts: a solution to the unforced equation and a particular solution that gives the oscillations due to the tides. Determine this particular solution using:
\[\delta_{\lambda p}=A \cos \left(v_{\theta} t+\phi+\theta\right)\]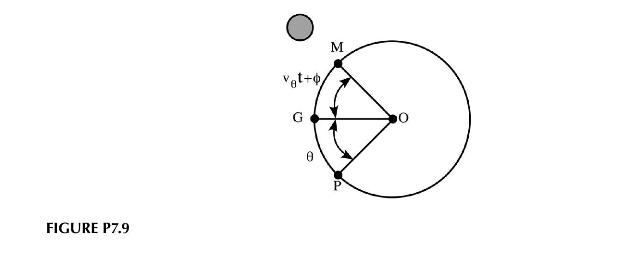
Step by Step Answer:






