We would like to look at a case of coupled transport: natural convection between horizontal walls. The
Question:
We would like to look at a case of coupled transport: natural convection between horizontal walls. The situation is shown in Figure P10.27. We assume that the length of the device is much larger than its height, i.e., \(v_{y} \approx 0\) and \(v_{x}=f(y)\).
a. Using the Boussinesq approximation for buoyant driven flow, show that the Navier-Stokes and energy equations can be reduced to the following set for this problem:
\[\begin{gathered}\frac{1}{ho} \frac{\partial P}{\partial y}=\beta_{T} g\left(T-T_{r e f}\right) \quad \frac{1}{ho} \frac{\partial P}{\partial x}=v \frac{\partial^{2} v_{x}}{\partial y^{2}} \\v_{x} \frac{\partial T}{\partial x}=\alpha\left(\frac{\partial^{2} T}{\partial x^{2}}+\frac{\partial^{2} T}{\partial y^{2}}\right)\end{gathered}\]
b. If the length of the device is much larger than its height, then:
\[\frac{\partial T}{\partial x} \approx \text { constant }(A) \text { i.e., } \Delta T \text { is constant }\]
Eliminate pressure from the set of equations above and show that:
\[\frac{\partial^{3} v_{x}}{\partial y^{3}}=\frac{\beta_{T} g}{v} A\]
c. Use the results of part
(b) to eliminate \(\partial^{2} T / \partial x^{2}\) and solve the energy and momentum equation to obtain the profiles.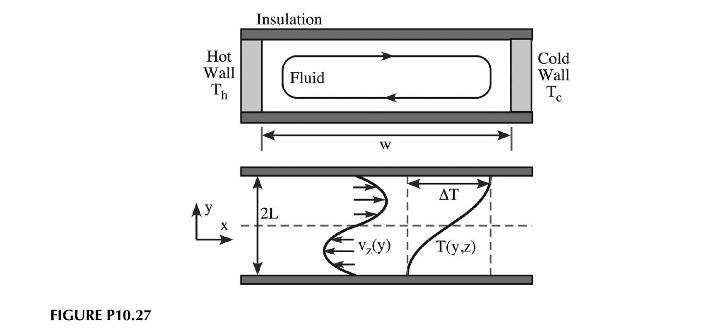
Step by Step Answer:






