Consider the two-dimensional tube of a noncircular cross section formed by rectangular and semicylindrical subdomains patched at the common dashed control surfaces in a manner similar to that described in Problem 4.59. Note that, along the dashed control surfaces, temperatures in the two subdomains are identical and local conduction heat fluxes to the semicylindrical subdomain are identical to local conduction heat fluxes from the rectangular subdomain. The bottom of the domain is held at T_s = 100 C by condensing steam, while the flowing fluid is characterized by the temperature and convection coefficient shown in the sketch. The remaining surfaces are insulated, and the thermal conductivity is k = 15 W/m · K.

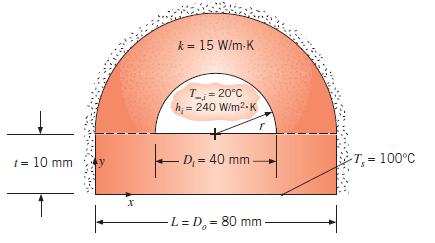
Find the heat transfer rate per unit length of tube, q, using Δx = Δy = Δr = 10 mm and Δϕ  =π/8.

Data From Problem 4.59

Conduction within relatively complex geometries can sometimes be evaluated using the finite-difference methods of this text that are applied to subdomains and patched together. Consider the two-dimensional domain formed by rectangular and cylindrical subdomains patched at the common, dashed control surface.

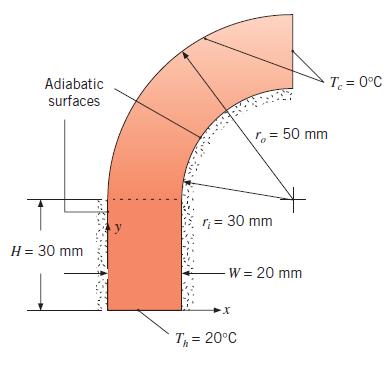
Calculate the heat transfer per unit depth into the page, q , using  Δx = Δy = r = 10 mm and Φ  =π/8. The base of the rectangular subdomain is held at T_h  = 20C, while the vertical surface of the cylindrical subdomain and the surface at outer radius r_o are at T_c = 0 C. The remaining surfaces are adiabatic, and the thermal conductivity is k = 10 W/m · K.

Transcribed Image Text:

t = 10 mm X k = 15 W/m-K T__, = 20°C h₁ = 240 W/m².K + D₁ = 40 mm -L= D = 80 mm- -T,= 100°C